들어가면서
세그먼트 트리를 연습하면서 문제를 도전했다. 아직 완벽히 내 것으로 만든 알고리즘이 아니라서 사소한 실수를 많이 했다.
문제를 풀면서 내가 한 실수들을 설명하고자 한다.
세그먼트 트리
서그먼트 트리는 데이터의 집합에서 특정 구간의 연산된 결과를 빠르게 구하기 위해서 사용하는 알고리즘 중에 하나이다.
비슷하게 사용되는 알고리즘으로는 누적합 알고리즘이 있다.
두 알고리즘은 목적이 같지만 상황에 따라서 더 효과적인 알고리즘이 있기 때문에 특성을 이해하고 사용하는 것이 좋다.
세그먼트 트리는 연산된 결과를 트리 형태로 미리 저장하는 알고리즘이다.
부모 노드의 값은 자식 노드들의 연산 결과로 구성되어 있다. 보통 이진트리 구조로 세그먼트 트리를 만들어 사용하는 것으로 보인다.
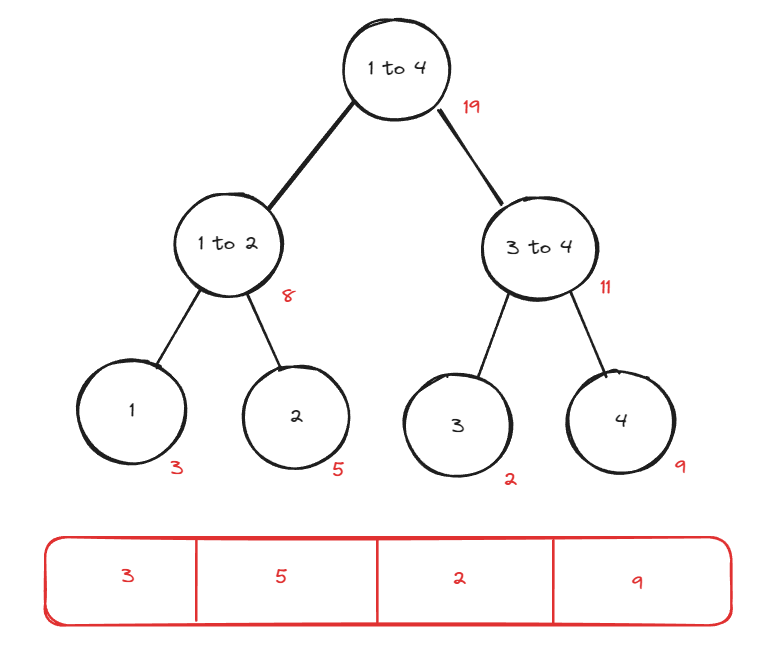
다음은 특정 범위의 값을 모두 더한 세그먼트 트리를 표현한 그림이다.
트리에는 특정 범위에 계산된 결과가 이미 계산되어 있어서 트리를 사용하면 어떤 범위의 누적합이든지 O(log N)의 시간 복잡도로 찾을 수 있다.
문제 요구사항
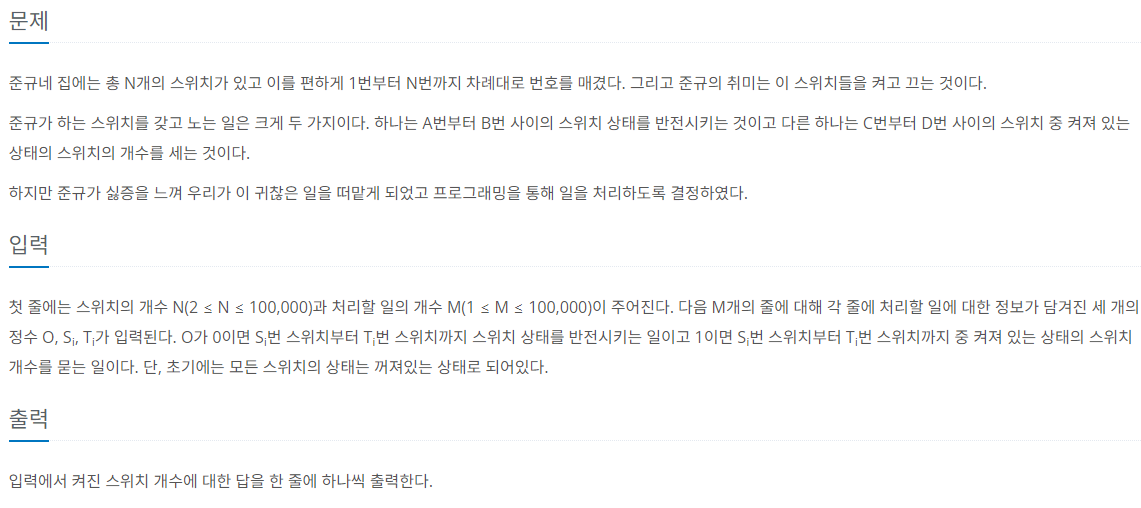
느리게 갱신하기
해당 문제를 풀려면 사용하는 방법인데 이것이 필요한 상황은 어떤 범위에 동일한 연산 결과를 적용하고 싶을 때이다.

예를 들면 3번째 값부터 4번째 값까지 범위에 있는 모든 요소를 10으로 변경하고 싶다면 그림에서처럼 해당 범위에 해당되는 노드들은 모두 값을 갱신해야한다. 하지만 이것은 갱신하고자 하는 범위가 최악의 상황에서 모든 범위로 확장한다고 생각하면 모든 노드들이 영향을 받는다. 즉 세그먼트 트리의 특징인 O(log N)의 성능이 보장되지 않느다.
그래서 느리게 갱신하는 전략을 사용한다. 이건 필요할 때 특정 노드의 값을 갱신하겠다는 전략이다.
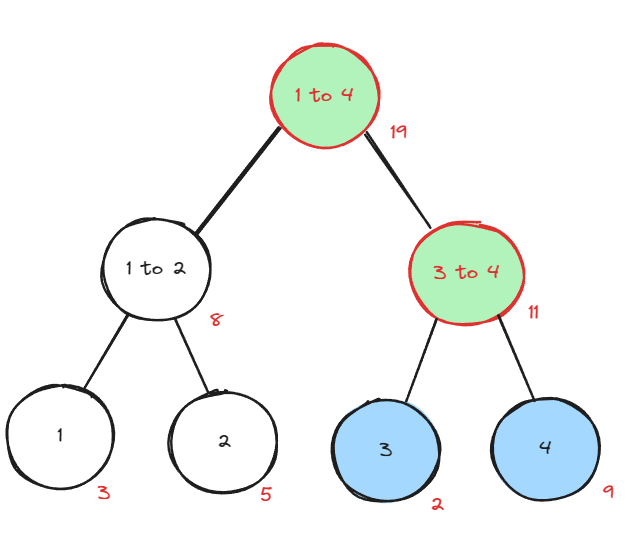
그림에서 보면 같은 3번째 값부터 4번째 값까지 범위를 갱신할 때 영향을 받는 초록 부분이 줄어들고 파란색으로 갱신 여부를 지연했다.
아직 이게 효율적이라는 생각이 들지 않는다면 모든 범위에서 갱신을 처리한 그림을 보자.
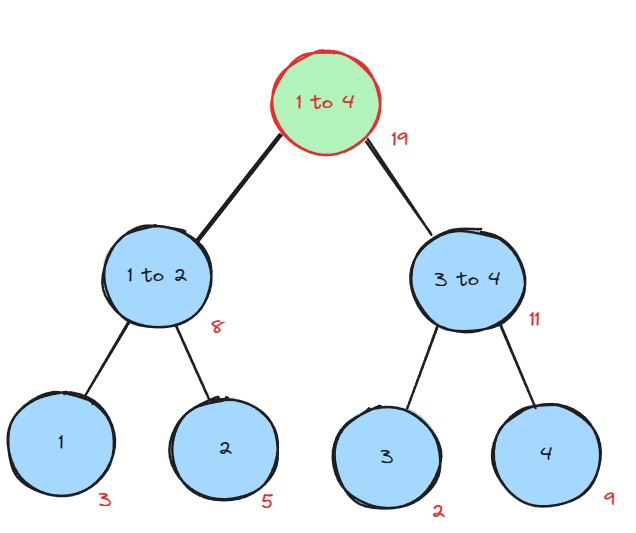
이 방법을 사용하면 노드를 사용하기 전에 갱신이 필요한지에 대한 정보와 어떻게 갱신을 해야 하는지에 대한 정보가 필요하다.
그래서 느리게 갱신하는 세그먼트 트리에는 이런 정보를 저장하는 변수가 하나 있다. 나는 lazy라는 이름의 배열을 사용해서 이 정보를 선언해서 문제를 풀었다.
실수들
- 갱신이 필요한 시그널을 잘못 설계했다.
갱신이 필요한 정보를 판단할 때, 모든 경우를 반영하지 않아서 문제를 틀렸다. - lazy의 자식 노드는 부모의 노드의 상태에 영향을 받지만 완전히 같은 상태는 아니다.
이 부분은 코드에서 주석 부분을 참고해 주기를 바란다.
static void lazyUpdate(int node, int start, int end) {
/*
1. 실수 : 업데이트가 있음을 알릴 때 lazy[node] != 0 으로 해서 0으로 업데이트를 진행하는 상황에서 무시가 되어서 이상하게 동작함
*/
if (lazy[node]) {
tree[node] = reverse(tree[node], start, end);
if (start != end) {
/*
2. 실수 : 부모의 노드라고 무조건 종속적인 관계가 아니다. 부모 노드가 lazy상태가 아닌데도 자식은 lazy 상태일 수 있기 때문이다.
*/
lazy[2 * node] = !lazy[2 * node];
lazy[2 * node + 1] = !lazy[2 * node + 1];
}
lazy[node] = false;
}
}후기

실수한 부분을 분석함으로써 세그먼트 트리를 사용할 때 좀 더 안정적으로 코드를 작성할 수 있을 것 같아서 뿌듯하다.
전체 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class B1395 {
static int[] switches;
static int[] tree;
static boolean[] lazy;
static void allocate(int size) {
int h = (int) (Math.ceil(Math.log(size) / Math.log(2)) + 1);
int treeSize = 1 << h;
tree = new int[treeSize];
lazy = new boolean[treeSize];
}
static int init(int node, int start, int end) {
if (start == end) return tree[node] = switches[start];
int mid = (start + end) / 2;
return tree[node] = init(2 * node, start, mid) +
init(2 * node + 1, mid + 1, end);
}
static int reverse(int value, int start, int end) {
return end - start + 1 - value;
}
static void lazyUpdate(int node, int start, int end) {
/*
업데이트가 있음을 알릴 때 lazy[node] != 0 으로 해서 0으로 업데이트를 진행하는 상황에서 무시가 되어서 이상하게 동작함
*/
if (lazy[node]) {
tree[node] = reverse(tree[node], start, end);
if (start != end) {
/*
부모의 노드라고 무조건 종속적인 관계가 아니다. 부모 노드가 lazy상태가 아닌데도 자식은 lazy 상태일 수 있기 때문이다.
*/
lazy[2 * node] = !lazy[2 * node];
lazy[2 * node + 1] = !lazy[2 * node + 1];
}
lazy[node] = false;
}
}
static void update(int node, int start, int end, int left, int right) {
lazyUpdate(node, start, end);
if (right < start || end < left) return;
if (left <= start && end <= right) {
tree[node] = reverse(tree[node], start, end);
if (start != end) {
lazy[2 * node] = !lazy[2 * node];
lazy[2 * node + 1] = !lazy[2 * node + 1];
}
return;
}
int mid = (start + end) / 2;
update(2 * node, start, mid, left, right);
update(2 * node + 1, mid + 1, end, left, right);
tree[node] = tree[2 * node] + tree[2 * node + 1];
}
static int sum(int node, int start, int end, int left, int right) {
lazyUpdate(node, start, end);
if (right < start || end < left) return 0;
if (left <= start && end <= right) return tree[node];
int mid = (start + end) / 2;
return sum(2 * node, start, mid, left, right) +
sum(2 * node + 1, mid + 1, end, left, right);
}
public static void main(String[] args) throws IOException {
var br = new BufferedReader(new InputStreamReader(System.in));
var input = new StringTokenizer(br.readLine());
int n = Integer.parseInt(input.nextToken());
int m = Integer.parseInt(input.nextToken());
switches = new int[n];
allocate(n);
init(1, 0, n - 1);
for (int i = 0; i < m; i++) {
input = new StringTokenizer(br.readLine());
int type = Integer.parseInt(input.nextToken());
int left = Integer.parseInt(input.nextToken()) - 1;
int right = Integer.parseInt(input.nextToken()) - 1;
if (type == 0) {// switch
update(1, 0, n - 1, left, right);
} else { // question
int sum = sum(1, 0, n - 1, left, right);
System.out.println(sum);
}
}
}
}
'ps' 카테고리의 다른 글
| [알고리즘] 스패닝 트리 (0) | 2023.10.14 |
|---|---|
| 최대공약수 구하기 (0) | 2023.04.25 |
| [프로그래머스] 고고학 최고의 발견 (0) | 2023.02.16 |
| [프로그래머스] 등대 (0) | 2023.02.16 |
| [프로그래머스] 퍼즐 조각 채우기 (0) | 2023.02.14 |
