프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
n개의 괄호 쌍을 가지고 짝이 맞는 문자열의 개수를 구하는 문제를 푸는 과정에서 알게 된 수열이다.
올바른 괄호에 카랄랑 수가 어떻게 적용되었는지를 생각해보았다.
c0 = 1 : ""
c1 = 1 : ()
c2 = 2 : ( () ), ( )( )
c3 = 5 : ( ( () ) ), ( ( )( ) ), ( )( )( ), ( () )( ), ( )( () )
올바른 괄호가 되기 위해서는 항상 양끝은 ( .... ) 꼴로 생성이 되어야한다. 그리고 ... 안에는 올바른 괄호가 들어오거나 (와 )의 순서가 딱 한번 잘못된 수열이 가능하다. 예를 들어 )(, )()(, () )( 와 같은 문자열이 있다.
또한 ...은 n-1개의 괄호쌍으로 구성되어있다.
그리고 올바른 괄호의 수열에서 처음에 '(' 문자를 뒤로 하나 보내면 순서가 딱 한 번 잘못된 문자열이 만들어진다.
c3 = c0 * c2 + c1 * c1 + c2 * c0 에 이러한 개념에 이를 적용하자
ci * cj 에서 ci는 문자열을 잘못만들었을 때의 문자열의 수 cj는 올바른 문자열의 수
c0 * c2 는 c0의 잘못된 문자열의 경우에 c2의 문자열을 더해서 만든 문자열의 수
c1* c1는 c1의 잘못된 문자열의 경우에 c1의 문자열을 더해서 만든 문자열의 수
c2 * c0 는 c2의 잘못된 문자열의 경웨 c0의 문자열을 더해서 만든 문자열의 수
다음 경우를 더해서 중복된 문자열이 나오지는 않는다. 왜냐하면 cn에서 올바른 문자열은 고유한 문자열이고 이를 역전한 잘못된 문자열 또한 고유한 문자열이다.
위와 같은 문제를 해결할 때 사용되는 수열이기도 하지만 유명한 다른 경우들도 있었다.
적용 문제
1. 다각형을 삼각형으로 나누는 방법을 구하기
2. n개의 괄호 문제
3. n+1 개의 리프노드를 갖는 이진트리의 개수를 구하기
점화식
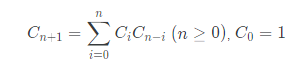

참고자료
카탈란수(CatalanNumber)
카탈란 수(Catalan Number) [Section2][Section3][Home] 2001.05.02 - made by sglee@math.skku.ac.kr and mass@math.skku.ac.kr 소개 [Introduction] 먼저 Catalan Number를 공부하기 전에 Catalan수를 발견한 Catalan에 대해서 알아보자. (Eug
matrix.skku.ac.kr
'etc' 카테고리의 다른 글
| Vim 유용한 명령어 팁 (2) | 2023.12.05 |
|---|---|
| 커스텀 스킨 셈플 (0) | 2023.11.05 |
| [windows] 윈도우에서 특정 사이트 접근 막는법! (0) | 2023.06.07 |
| 가상머신 팁 모음 (0) | 2023.06.03 |
| 리눅스 명령어 모음 (0) | 2023.04.17 |
